Conditions de stabilité
HullCAO 5.0 Online help - Eric COLLARD
 
Niveau de difficulté     1   2   3 
Si, partant de la position d’équilibre ainsi définie, le navire est soumis à « une sollicitation qui tend à l’en écarter » (par exemple pour un voilier, l’action du vent sur la voilure), le flotteur tendra à prendre une inclinaison qui entraînera une modification de la position du centre de carène B, et par conséquent, un décalage des supports de la poussée d’Archimède et du poids. En effet l’inclinaison ne modifie pas la condition de flottabilité, mais les formes de carènes sont telles que l’inclinaison rend habituellement dissymétriques les sections immergées, faisant passer le centre de carène du plan de symétrie vers le bord incliné. Poussée d’Archimède et poids constituent un couple (forces parallèles d’égales intensités et de directions opposées) caractérisé par son moment (produit de l'intensité de la force: poids du navire - ou son déplacement - par la distance entre leurs supports, ou «bras de levier »). Considérant par exemple une inclinaison transversale - gîte d’angle θ (direction d’inclinaison normalement la plus «sensible » à cause de la forme allongée du navire) - les schémas suivants montrent, par référence à la verticale d’origine (axe de symétrie du navire), que trois cas de figures peuvent se présenter, selon la position du centre de gravité G en hauteur, pour un flotteur (ou carène) donné :

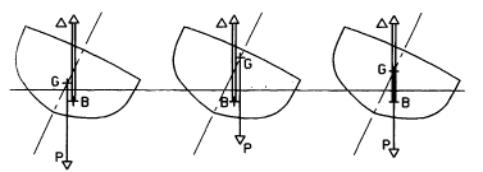
    STABLE                 INSTABLE                          NEUTRE

  1. le centre de carène se déplace plus loin vers le bord incliné que la verticale passant par le centre de gravité. Le couple des forces « poids - poussée d’Archimède » génère un moment qui tend à s’opposer à la « force inclinante » (si on « libère » la force inclinante, le navire tend à se redresser) : l’équilibre est stable, le moment correspondant s’appelle « moment de redressement ».
  2. le centre de carène se déplace moins loin que la verticale passant par le centre de gravité. Le couple des forces « poids - poussée d’Archimède » génère un moment qui tend à augmenter l’inclinaison (si on libère la force inclinante, le navire tend à s’incliner davantage, et à l’extrême chavirer) : l’équilibre est instable.
  3. entre ces deux figures: le centre de carène se déplace exactement à la verticale du centre de gravité. Le couple des forces « poids - ­poussée d’Archimède » génère un moment qui est nul à nouveau (bras de levier nul, comme à l’inclinaison 0°) : l’équilibre est neutre.

Dans ces figures, le « bras de levier » est représenté par la distance horizontale qui sépare le centre de gravité G et sa projection sur la verticale passant par le centre de carène, traditionnellement désignée par la lettre « Z ». Il s’appelle donc « GZ ». On le compte positif s’il correspond à un moment de redressement (cas 1), négatif dans le cas contraire (cas 2). Le moment du couple s’écrit:

Mt = P.GZ = Δ.GZ (N.m ou souvent t.m)

Etude de la stabilité courbe des bras de levier

On analyse l’ensemble de la stabilité du navire, c’est à dire pour toutes les inclinaisons possibles (sans dépasser, en général, 180° pour raison de symétrie, voire moins pour certains types de navires) en établissant une courbe où sont portés en abscisses les angles d’inclinaison θ, et en ordonnées les bras de levier « GZ » correspondants. Cette courbe, qui caractérise la stabilité d’un navire (considéré dans une situation de chargement donnée) est appelée courbe des bras de levier de redressement (N.B. on représente parfois la courbe des moments correspondants, évidemment identique à celle des bras de levier au facteur déplacement près).

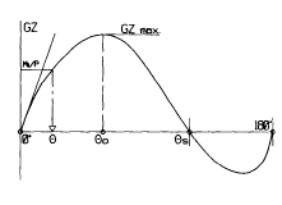La figure ci-contre schématise une courbe de bras de levier typique. A l’inclinaison 0°, le bras de levier (GZ) est nul (pour raison de symétrie et sauf exception). Puis sa valeur augmente avec l’inclinaison jusqu’à un maximum atteint pour un angle θ0 appelé angle limite de stabilité statique. A partir de cette valeur, le bras de levier diminue jusqu’à atteindre à nouveau la valeur zéro pour un angle θs appelé angle de chavirement statique. Puis les valeurs devenues négatives, décroissent encore jusqu’à un minimum pour remonter enfin jusqu’à la valeur zéro à nouveau à 180° (pour la même raison de symétrie qu’à 0°).


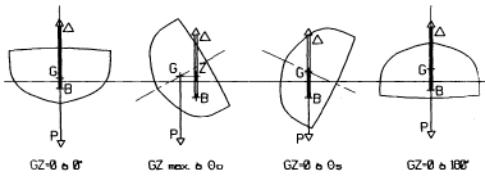
Les figures précédentes sont établies en supposant le flotteur entièrement étanche, pour toutes les inclinaisons, ce qui n’est généralement pas le cas. On définit donc aussi un angle de début d’envahissement θf, qui est celui à partir duquel l’eau peut pénétrer librement à l’intérieur de la coque par une ouverture quelconque. Enfin, on définit encore un angle limite de stabilité « dynamique » θd, qui correspond à l’équilibre des énergies supposées nécessaires pour d’une part amener le flotteur à cette inclinaison et d’autre part pour lui permettre d’y résister en fonction des caractéristiques propres du navire. Ces angles θf et θd font l’objet pour certaines catégories de navires de restrictions réglementaires.

Si on connaît la valeur d’une force appliquée au navire, à laquelle correspond un moment inclinant Mi, la courbe des bras de levier permet de connaître immédiatement l’inclinaison θ correspondante (équilibre des moments) en reportant en ordonnée sa valeur rapportée en terme de GZ équivalent (Mi/P).