Metacentre
HullCAO 5.0 Online help - Eric COLLARD
 
Level of difficulty     1   2   3 
Between the position of origin of the float (slope = 0°) and an unspecified position of slope, the center of hull B describes in space a trajectory which brought it its initial position (located in the longitudinal plan) to that (shifted longitudinal plan) corresponding to the slope. Considering, to leave and on both sides the slope a light variation of slope, one can imagine that B describes an arc of curve which, if it is sufficiently small, can be compared to an arc of circle whose center is the " metacentre M relating to the slope ". The radius of the corresponding circle is called the radius metacentric: it is named "R" in the case of a purely transverse slope, " R " in the case of a purely longitudinal slope, and " " in the case, more general, of an unspecified slope (more or less oblique). M is thus the instantaneous centre of rotation of the float (considered on a perfectly calm water level and very slow movement). The knots M and B are different for each slope, and thus which one shows (formula of Bouguer) that the value is equal, for a given slope, with the relationship between the moment of inertia of the surface of floating inclined compared to the hingepin corresponding (X) and immersed volume is:

(m) = IX (m4)/ V (m3)

For a transverse slope:

R = IT / V

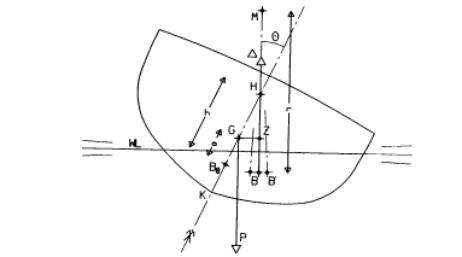
In the figure below, the intersection H of the vertical passing by the center of hull B with the longitudinal plan of the ship is called the transverse knot metacentric relating to the slope , and its distance " H " in the center of hull in the beginning B0, the corresponding metacentric height.The centre of gravity of the ship G is located by its distance " has " in the center of hull origin B0.Balance is thus stable if ha is positive, i.e. if G is located below H, unstable in the contrary case. The metacentre M is located on vertical BH. The arm of lever GZ of the couple of the forces P and A is obtained according to the angle considered by the relation:

GZ = GH.sin = (h-a).sin

and moment corresponding:

MT = P.GZ = P.(h-a).sin

The curve of the arms of lever is plotted today for the majority of the ships by average data processing, starting from a model of sufficiently precise forms (complete float including the dead works tight, i.e. considered as noninvadable), for which one fixes a value of displacement, or weight of the ship and the corresponding position of its centre of gravity. For each successive slope, the position of the center of hull, or more precisely isocarene (i.e. including the possible corrections of plate) is recomputed, and thus the arm of corresponding lever. But one cannot wait, in general, to be returned of it at the stage of the data-processing seizure to have an idea would be this only approximate, of the stability of a future ship in project. It will be often necessary to at least make an investigation preliminary on this subject dice the first outlines.